Tetraxis® Magnetic Geometry Puzzle
Step-by-Step Assembly Instructions
Step-by-Step Assembly Instructions
If you need help figuring out how to put the Tetraxis® puzzle together, the pictures below will walk you through it. This is just one of many possible sequences of steps.
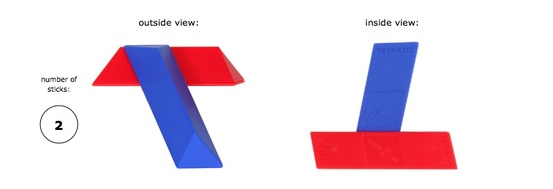
It helps to keep in mind that any two sticks that touch relate to each other in the same way:
Add a third stick to form one quarter of the puzzle. When looking at the outside of the puzzle, notice how the blue stick overlaps the red stick in exactly the same way as the red stick overlaps the yellow, and as the yellow overlaps the blue.
Now add a fourth stick:
Here is an alternative grouping of four sticks, also a good way to start assembling the Tetraxis puzzle.
Either way leads to this configuration of five sticks when you add a red stick:
Now keep adding sticks one at a time:
You see that hollow space forming in the middle?
When you finish the puzzle, that space will have 12 sides (faces), 14 corners (vertices), and 24 edges. The shape is called a rhombic dodecahedron.
Each face is a rhombus. To see another curious occurrence of this same rhombus in each stick of the puzzle, click here.

In the assembly shown above, sticks are arranged by color so that any three sticks that point in the same direction are the same color.
Can you assemble the puzzle so that no two sticks pointing in the same direction are the same color?
How many ways can you choose three different colors to make triangular configurations like the one shown to the right? Can you assemble the puzzle so that all combinations appear?
(The most common answers are 4 and 8. Depending on how you define color combinations as being different, both answers are correct.)
How many ways can you use all four colors to make “pinwheel” configurations as shown below? For example, blue over green over red over yellow is shown here.
A different combination would be blue over green over yellow over red. Look for all combinations in a fully assembled Tetraxis® puzzle.
Can you assemble the puzzle so that no two sticks pointing in the same direction are the same color?
How many ways can you choose three different colors to make triangular configurations like the one shown to the right? Can you assemble the puzzle so that all combinations appear?
(The most common answers are 4 and 8. Depending on how you define color combinations as being different, both answers are correct.)
How many ways can you use all four colors to make “pinwheel” configurations as shown below? For example, blue over green over red over yellow is shown here.
A different combination would be blue over green over yellow over red. Look for all combinations in a fully assembled Tetraxis® puzzle.